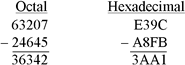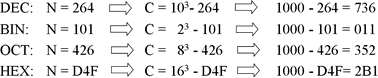Sistemas de numeração |
||||||||||||||
|
Roteiro de aulas práticas
Sumário:
|
||||||||||||||
|
Sistemas de numeração Os sistemas de numeração dividem-se em dois grandes grupos: sistemas numéricos posicionais e sistemas numéricos não-posicionais. Posicionais – o valor atribuído ao símbolo depende da posição que ele ocupa em relação ao conjunto.
Exemplo extraído do sistema decimal:
Todos os sistemas numéricos posicionais são identificados por uma base.
Não-posicionais – os símbolos possuem valores definidos e imutáveis, não dependendo da posição que ocupam no conjunto de que fazem parte. Exemplo utilizando algarismos romanos:
O símbolo V encontrado nos três conjuntos acima tem um valor constante (5), embora ele tenha variado de posição em cada conjunto. No primeiro conjunto o algarismo romano V ocupa a primeira e única posição, no segundo, ele ocupa a segunda posição a contar da direita para a esquerda e no terceiro conjunto, ocupa a posição de número três. Como se vê, o algarismo muda de posição mas seu valor continua imutável, não depende, portanto, de sua posição em relação ao conjunto.
Os seguintes sistemas de numeração posicionais são alvos desse estudo:
|
||||||||||||||
|
Conversões: 1o) De qualquer base para a decimal 1º método: Aplicando o Teorema Fundamental da Numeração que relaciona uma quantidade expressa num sistema de numeração qualquer com a quantidade equivalente expressa no sistema decimal.
Exemplo 1: converter o no binário inteiro: 1101. 11012 = (1 x 23 + 1 x 22 + 0 x 21 + 1 x 20)10
11012 = (8 + 4 + 0 + 2)10
11012 = 1310
Exemplo 2: converter o no real binário: 10111,011.
10111,0112 = (1x24 + 0x23 + 1x22 + 1x21 + 1x20 + 0x2-1 + 1x2-2 + 1x2-3)10
10111,0112 = (16 + 0 + 4 + 2 + 1 + 0 + 0,25 + 0,125)10
10111,0112 = 23,37510 2º método: Determinando os valores de posições.
Determinar os valores de posições de cada algarismo do número dado e multiplicar cada qual pelo valor de posição correspondente. Exemplo 3: converter o no octal 3547. 83 82 81 80 (valores de posições)
512 64 8 1 (valores de posições)
3 5 4 7 (número dado) 35478 = (3 x 512 + 5 x 64 + 4 x 8 + 7 x 1)10
35478 = 189510
Exemplo 4: converter o no binário: 1100.
Este método é bastante prático para converter binário em decimal, pois basta efetuar a soma do valor da posição onde aparece o dígito 1 no número dado.
3º método: Multiplicando e somando. Multiplicar o 1o algarismo da esquerda pela base de origem, somar o algarismo seguinte a este produto, multiplicar novamente pela base e somar o algarismo seguinte e assim, sucessivamente, até somar o último algarismo da direita.
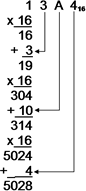
Exemplo 5: converter o no hexadecimal 13A4.
2o) Da decimal para qualquer base Efetuar divisões sucessivas pela base de destino até zerar o quociente. O resultado é formado pelos restos da divisões, tomados a partir do último resto para o primeiro.
Exemplo 1: converter o no 258 para o sistema octal. 258 : 8 = 32 : 8 = 4 : 8 = 0
Restos: 2 0 4
Portanto, 25810 = 4028
Exemplo 2: converter o no 40,375 para binário. Para a parte inteira efetuar divisões sucessivas por 2: 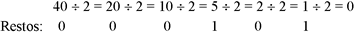 4010 = 1010002 4010 = 1010002Para a parte fracionária efetuar multiplicações sucessivas por 2, considerando como resultado a parte inteira dos produtos:
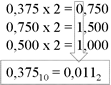 Juntando as partes inteira e fracionário, têm-se: 40,37510 = 101000,0112 |
||||||||||||||
|
3o) Conversões entre sistemas binário, octal e hexadecimal: a) Binário para Octal e Octal para Binário
Determinar grupos de três algarismos binário a cada algarismo octal, iniciando na vírgula decimal. Depois efetuar a conversão dos grupos individuais como se fosse de binário para decimal e vice-versa.
Exemplos:
Bin para Oct: 111110010,1 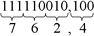 Logo: 111110010,12= 762,48 Logo: 111110010,12= 762,48Oct para Bin: 5403 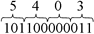 Logo: 54038 = 1011000000112 Logo: 54038 = 1011000000112b) Binário para Hexadecimal e Hexadecimal para Binário Fazer corresponder grupos de quatro algarismos binários a cada símbolo hexadecimal, a partir da virgula decimal.
Em seguida, efetuar a conversão dos grupos individuais como se fosse de binário para decimal e vice-versa.
Exemplos:
Bin para Hex: 1110101101,010 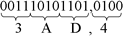 Logo: 1110101101,0102 = 3AD,416 Logo: 1110101101,0102 = 3AD,416 Hex para Bin: F9,E 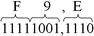 Logo: F9,E16 = 11111001,11102 Logo: F9,E16 = 11111001,11102c) Octal para Hexadecimal e Hexadecimal para Octal Converter primeiro para binário e, em seguida, de binário para hexadecimal ou octal.
Exemplos:
Oct para Hex: 617,2 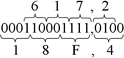 Logo: 617,28 = 18F,416 Logo: 617,28 = 18F,416 Hex para Oct: 8C,B 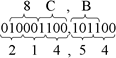 Logo: 8C,B16 = 214,548 Logo: 8C,B16 = 214,548Exercícios de conversões:
Execute os exercícios e confira os resultados utilizando o programa Conversão de sistemas numéricos. |
||||||||||||||
|
Operações aritméticas – adição Procedimento: Efetuar a soma da coluna do mesmo modo que no decimal. Se a soma for menor que o valor da base do sistema em operação, colocar o resultado na coluna considerada, caso contrário, dividir a soma da coluna pelo valor de base do sistema, obtendo-se um quociente inteiro e um resto. Escrever o resto como valor da coluna e o quociente como transporte para a soma da coluna seguinte.
Exemplo: BIN: 110110 + 11111 + 110111 = 10001100
Demonstração: 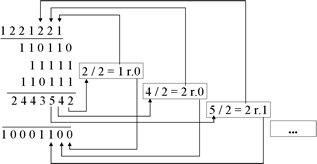 Exemplos: Procedimento igual ao mostrado no exemplo anterior, mudando-se apenas o valor do divisor de acordo com a base considerada. |
||||||||||||||
|
Operações aritméticas – subtração Exemplo: BIN: 110001 – 10111 = 11010
Demonstração:  Procedimento: Proceder do mesmo modo que no sistema decimal. Iniciar a subtração dos algarismos da coluna à direita e continuar com os algarismos da coluna imediatamente à esquerda e seguindo esta ordem até ancançar a última columa mais à esquerda, efetuando as seguintes operações: Primeira coluna: 1 – 1 = 0, registrar este valor na linha de resto ou resultado; Segunda coluna: 0 – 1, como o minuendo é menor, tomar uma base emprestada do minuendo da terceira coluna, ficando o minuendo desta com –1, registrado na linha do minuendo modificado e na linha de empréstimo de base, o número 2. Resultado da coluna: 2 – 1 = 1; Terceira coluna: –1 – 1, como o minuendo é menor, tomar uma base emprestada do minuendo da quarta coluna, ficando o minuendo desta com –1, registrado na linha do minuendo modificado e na linha de empréstimo de base, o número 2. Resultado da coluna: 2 –1(minuendo modificado) – 1 = 0; Quarta coluna: –1 – 0, como o minuendo é menor, tomar uma base emprestada do minuendo da quinta coluna, ficando o minuendo desta com 0, registrado na linha do minuendo modificado e na linha de empréstimo de base, o número 2. Resultado da coluna: 2 –1(minuendo modificado) – 0 = 1; Quinta coluna: 0 – 1, como o minuendo é menor, tomar uma base emprestada do minuendo da sexta coluna, ficando o minuendo desta com 0, registrado na linha do minuendo modificado e na linha de empréstimo de base, o número 2. Resultado da coluna: 2 – 1 = 1; Sexta coluna: Resultado da coluna: 0 – 0 = 0. Exemplos: Procedimento semelhante ao apresentado no exemplo anterior, modificando-se apenas o empréstimo de base para o valor da base considerada, contemplando o valor 8 para o octal e 16 para o hexadecimal. |
||||||||||||||
|
Operações aritméticas – multiplicação Multiplicar cada dígito do multiplicador a partir da direita por todos os dígitos do multiplicando e somar as parcelas dos produtos, como se procede no sistema decimal.
Exemplo do sistema Octal: 6320,7 x 4,5. (6320,7 é o multiplicando e 4,5 é o multiplicador) Demonstração:
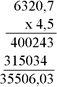 Procedimento:
5 x 7 = 35. 35 é um número do sistema decimal. Como se está trabalhando com o sistema octal, esse número deve ser dividido pela base do sistema que neste caso é 8. Então, 35 / 8 = 4 r.3. O resto 3 corresponde ao primeiro dígito da primeira parcela e o quociente 4 é o transporte a ser somado ao produto de 5 x 0 que resultará em 4, obtendo-se, assim, o segundo dígito da primeira parcela. E, desse modo, continuar essas operações até esgotar os algarismos do multiplicando. Após obter a segunda parcela, tendo como multiplicador o número 4, efetua-se a soma das parcelas e posiciona-se a vírgula decimal. Exemplos: 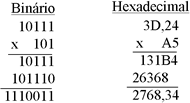 Procedimento análogo ao mostrado no exemplo anterior, sendo que no sistema binário a multiplicação é bastante simples porque tem-se apenas o algarismo nulo e o neutro. Para o sistema hexadecimal considera-se o valor 16 em vez de 8 utilizado no método do exemplo anterior. |
||||||||||||||
|
Operações aritméticas – divisão Exemplo do sistema binário:
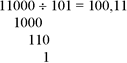 Procedimento: A forma mais simples é converter os valores envolvidos em cada passo da operação para o decimal. Os três primeiros algarismos, da esquerda para a direita, tem valor 110 (= 6 no decimal) maior que o quociente 101 (= 5 no decimal). Efetuando-se a divisão obtém-se quociente 1 e resto também 1. Em seguida o próximo algarismo do dividendo é baixado ao lado do resto configurando-se no valor 10 e como este é menor que o divisor coloca-se 0 no quociente e é baixado o próximo algarismo, passando o resto agora a representar o valor 100, que ainda é menor que o divisor, razão pela qual o quociente recebe mais um 0. Nesta altura, todos os algarismos do dividendo já foram considerados no cálculo. Vamos continuar o processo de divisão, apondo uma vírgula no quociente (100,) e 0 à direita do resto perfazendo o valor 1000 (= 8 no decimal) que dividido por 101 (= 5 no decimal) resulta no queociente 1 e no resto 11 (= 3 no decimal). Para continuar a divisão coloca-se 0 à direita do resto que se torna agora 110 (= 6 no decimal) e efetuando a divisão (110/101, em decimal 6/5 ), obtém-se 1 como quociente e 1 como resto.
Exemplos dos sistemas octal e hexadecimal: 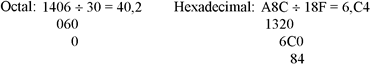 Procedimento análogo a operação de divisão realizada no sistema binário com a diferença da base, convertendo para decimal a fim de realizar a divisão e reconvertendo o quociente e o resto da divisão para o sistema considerado. |
||||||||||||||
|
Aritmética complementar – complemento Complementos: A base
A base – 1
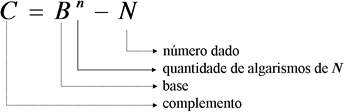
 Fórmula do complemento a base:
Exemplos de complementos aritméticos:
|
||||||||||||||
|
Aritmética complementar – subtração Para efetuar operações de subtração por meio da aritmética complementar, proceda como segue:1o) achar o complemento do subtraendo;
2o) somar o complemento ao minuendo:
Numeros decimais com resultados positivos:
Demonstração do cálculo 76 – 34:
Dessa forma, entende-se que computadores providos com apenas circuitos somadores são capazes de efetuar todos os tipos de operações aritméticas.
No caso da subtração, visto anteriormente, a apuração do complemento do subtraendo pelo computador seria efetuada somando uma unidade ao subtraendo tantas vezes quantas forem necessárias para atingir o módulo imediatamente superior ao valor inicial do subtraendo e o resultado é obtido pelo número de unidades adicionadas.
Por exemplo, o módulo superior do número 34 é 100, de 108 é 1000, de 2610 é 10000 e assim por diante, ou seja, refere-se a potência imediatamente superior do número considerado. No 1º exemplo, é 102, no 2º, é 103 e no 3º, é 104.
É importante observar que, antes de iniciar a operação, deve-se alinhar a quantidade de algarismos do subtraendo com a do minuendo de modo a conterem o mesmo número de algarismos. Por exemplo, na operação complementada 68 – 5, alinhando o subtrendo com o minuendo fica 68 – 05. Assim, o módulo imediatamente superior do subtraendo é 100 e não 10 como se poderia supor.
Números decimais com resultados negativos:
Números binários com resultados positivos:
Exemplo: |
||||||||||||||
|
Aritmética complementar – divisão Procedimento: 1o) achar o complemento do divisor;
2o) efetuar somas sucessivas do complemento do divisor ao dividendo até que o resultado da soma complementada seja inferior ao divisor, constituindo-se no resto;
3o) contar a quantidade de adições realizadas, cujo valor corresponderá ao quociente.
Se o resto (resultado da soma complementada) for diferente de 0 (zero) pode-se continuar a operação, porém antes deve-se multiplicar o resto pela base do sistema e uma vírgula é colocada no quociente ao final da 1ª série de multiplicação. Nas próximas multiplicações pela base o quociente que corresponde ao numero de multiplicações é acrescentado como uma casa decimal à direita do quociente anterior. Exemplo: decimal: 48 ÷ 15 = 3,2.
Demonstração:
 Exemplo: hexadecimal: 3C ÷ 14 = 3
Demonstração:
 |
||||||||||||||
|
Bibliografia
Eletrônica:
|
||||||||||||||